جواب فصل هفتم ۷ ریاضی پنجم (آمار و احتمال)

پاسخ درس هفتم ریاضی کلاس پنجم (آمار و احتمال)

راهنمای کامل حل تمرین‌های فصل هفتم

این بخش به شما کمک می‌کند تا پاسخ پرسش‌ها و فعالیت‌های درس «آمار و احتمال» را به صورت مرحله‌به‌مرحله بررسی کنید.

**مفاهیم اصلی این فصل:**

* **آمار:** روشی برای جمع‌آوری، دسته‌بندی و نمایش اطلاعات تا بتوانیم آن‌ها را بهتر بفهمیم.
* **احتمال:** پیش‌بینی این است که یک اتفاق چقدر امکان رخ دادن دارد.

**روش‌های نمایش اطلاعات:**

برای نشان دادن اطلاعات از روش‌های مختلفی استفاده می‌شود، مانند:
* **نمودار تصویری:** در این نمودار از شکل‌ک‌ها یا نمادها برای نشان دادن تعداد استفاده می‌شود.
* **نمودار ستونی:** اطلاعات با استفاده از ستون‌های بلند و کوتاه نشان داده می‌شوند. هرچه ستون بلندتر باشد، تعداد بیشتر است.
* **نمودار خط‌شکسته:** این نمودار تغییرات اطلاعات در طول زمان را با اتصال نقطه‌ها به یکدیگر نشان می‌دهد.

**چگونه احتمال را اندازه‌گیری کنیم؟**

احتمال رخ دادن یک اتفاق را با کسری ساده نشان می‌دهیم:

**تعداد حالت‌های مورد نظر ÷ تعداد کل حالت‌های ممکن**

برای مثال، وقتی یک تاس معمولی را می‌اندازید:
* احتمال آمدن عدد ۳ می‌شود: ۱ تقسیم بر ۶ (چون فقط یک صورت تاس عدد ۳ دارد و در کل شش وجه وجود دارد).
* احتمال آمدن یک عدد زوج می‌شود: ۳ تقسیم بر ۶ (چرا؟ چون اعداد ۲، ۴ و ۶ زوج هستند؛ یعنی سه حالت مورد نظر داریم).

با مطالعه این راهنما و حل دوباره تمرین‌ها می‌توانید مطمئن شوید که مفاهیم این درس را به خوبی یاد گرفته‌اید.

**عنوان درس:** آمار و احتمال
**مبحث:** یادگیری مرحله به مرحله
**پایه:** پنجم دبستان

در این درس، با دو مفهوم ساده و کاربردی به نام‌های “آمار” و “احتمال” آشنا می‌شویم. این مفاهیم به ما کمک می‌کنند تا اطلاعات را منظم کنیم و درباره اتفاقات آینده، پیش‌بینی‌های منطقی داشته باشیم.

**آمار چیست؟**
گاهی اوقات، ما اطلاعات زیادی درباره یک موضوع جمع‌آوری می‌کنیم. برای مثال، ممکن است بخواهیم بدانیم که بچه‌های کلاس ما چه میوه‌ای را بیشتر دوست دارند. آمار به ما یاد می‌دهد که چگونه این اطلاعات را به صورت منظم درآوریم، آن‌ها را دسته‌بندی کنیم و سپس با استفاده از نمودارهایی مثل نمودار ستونی یا تصویری، به شکلی ساده نشان دهیم. وقتی اطلاعات را در نمودار می‌بینیم، فهمیدن و مقایسه کردن آن‌ها بسیار آسان‌تر می‌شود.

**احتمال چیست؟**
احتمال به این معناست که چقدر امکان دارد یک اتفاق خاص بیفتد. ما در زندگی روزمره همیشه از احتمال استفاده می‌کنیم. برای مثال، وقتی به آسمان نگاه می‌کنیم و ابرهای تیره می‌بینیم، احتمال می‌دهیم که به زودی باران ببارد. احتمال را معمولاً با کلماتی مانند “حتماً”، “ممکن است” یا “بعید است” بیان می‌کنیم. در ریاضی، برای نشان دادن احتمال از اعداد بین صفر و یک استفاده می‌شود. اگر احتمال یک اتفاق صفر باشد، یعنی آن اتفاق هیچ وقت نمی‌افتد و اگر احتمال آن یک باشد، یعنی حتماً اتفاق می‌افتد.

**جمع‌بندی:**
به طور خلاصه، آمار مانند یک ابزار نظم‌دهنده برای اطلاعات گذشته و حال ماست و احتمال مانند یک پیش‌بینیکننده برای اتفاقات آینده. یادگیری این دو مفهوم به ما کمک می‌کند تا دنیای اطراف خود را بهتر درک کنیم و تصمیم‌های بهتری بگیریم.

گام به گام درس هفتم ریاضی پنجم ابتدایی

منوی دسترسی سریع:
راهنمای کامل فصل هفتم ریاضی پایه پنجم

پاسخ فعالیت صفحه ۱۲۶ ریاضی پنجم
پاسخ تمرین های کلاسی صفحه ۱۲۷ ریاضی پنجم
پاسخ فعالیت صفحه ۱۲۸ ریاضی پنجم
پاسخ سوالات صفحه ۱۲۹ ریاضی پنجم
پاسخ فعالیت صفحات ۱۳۰ و ۱۳۱ ریاضی پنجم
پاسخ تمرین های کلاسی صفحه ۱۳۱ ریاضی پنجم
پاسخ فعالیت صفحه ۱۳۲ ریاضی پنجم
پاسخ مسائل صفحه ۱۳۳ ریاضی پنجم
پاسخ فعالیت صفحه ۱۳۴ ریاضی پنجم
پاسخ تمرین های کلاسی صفحه ۱۳۵ ریاضی پنجم
پاسخ فعالیت صفحه ۱۳۶ ریاضی پنجم
پاسخ تمرین های کلاسی صفحه ۱۳۶ ریاضی پنجم
پاسخ مسائل صفحه ۱۳۷ ریاضی پنجم
پاسخ بخش فرهنگ نوشتن صفحات ۱۳۸ و ۱۳۹ ریاضی پنجم

راهنمای جامع فصل هفتم ریاضی پایه پنجم – شامل پاسخ تمام فعالیت‌ها، تمرین‌های کلاسی و مسائل صفحات ۱۲۶ تا ۱۳۹ کتاب درسی

جواب فعالیت صفحه ۱۲۶ فصل هفتم ریاضی پنجم دبستان

پویا از رفقایش پرسید که در روزهای تعطیل چقدر وقت برای بازی می‌گذارند. سپس پاسخ‌های آن‌ها را در جدول کناری یادداشت کرد. به این اطلاعات، «داده» و به این نوع جدول، «جدول داده‌ها» می‌گویند.

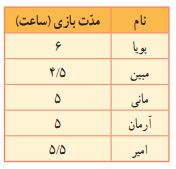
الف) پویا بیشتر از بقیه بازی کرده است.
ب) مبین کمتر از بقیه بازی کرده است.
پ) بین اعداد موجود، عدد ۵ بیشتر از بقیه تکرار شده و دو بار دیده می‌شود.
ت) مانی و مبین هر کدام یک نمودار ستونی بر اساس اطلاعات جدول کشیده‌اند. لطفاً به این نمودارها با دقت نگاه کنید.
عنوان هر نمودار و نام محورهای افقی و عمودی آن را نیز مطالعه کنید.

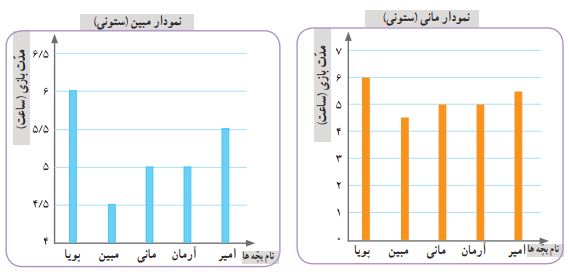
در ادامه، نمودارهای «مبین» و «مانی» را با هم مقایسه می‌کنیم. شباهت‌ها و تفاوت‌های آن‌ها را بیان می‌کنیم.

تفاوت: در نمودار مبین، اعداد روی محور عمودی از عدد ۴ شروع شده‌اند. اما در نمودار مانی، اعداد از صفر آغاز می‌شوند.

شباهت: هر دو نمودار از نوع ستونی هستند و یک مجموعه اطلاعات یکسان را نمایش می‌دهند.

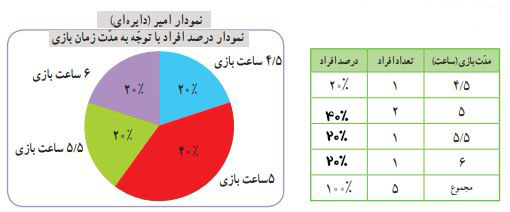
امیر نیز با استفاده از جدول زیر، یک نمودار جدید کشیده است.

پ) حالا جدول زیر را کامل کنید.

جواب کار در کلاس صفحه ۱۲۷ فصل ۷ ریاضی پنجم دبستان

نمایشگاه بین‌المللی کتاب تهران، همه‌ساله در ماه اردیبهشت برپا می‌شود. آقای بهاری سال قبل در این نمایشگاه، یک غرفه برای فروش بستنی دایر کرده بود. او هر روز مقدار فروشش را ثبت و یادداشت می‌کرد. نموداری که در ادامه می‌بینید، توسط آقای بهاری برای نمایش میزان فروش در یکی از روزهای نمایشگاه ترسیم شده است.

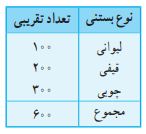
بر اساس جدولی که مشاهده می‌کنید، نمودار دایره‌ای روبرو را تکمیل کنید.
هر بخش از این دایره، معادل ۱۰۰ بستنی است.

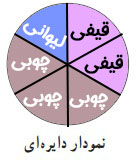
ب) به نظر شما آقای بهاری با نوشتن این اطلاعات چه سودی می‌برد؟
او می‌تواند با نگاه کردن به این اطلاعات متوجه شود که کدام نوع بستنی مشتریان بیشتری دارد و مردم بیشتر آن را می‌پسندند و کدام بستنی کم‌تر خریداری می‌شود.

دانش‌آموزان پایه پنجم و ششم یک محله، برای شرکت در کلاس‌های سفالگری و نجاری، نام‌نویسی خود را در سرای محله انجام داده‌اند. آمار مربوط به تعداد شرکت‌کنندگان در هر کلاس، در نمودارهای زیر نشان داده شده است.
در هر کدام از این دوره‌ها در مجموع ۴۰ نفر ثبت‌نام کرده‌اند. دانش‌آموزان کلاس پنجمی در کدام یک از این کلاس‌ها بیشتر نام‌نویسی کرده‌اند؟ در کلاس نجاری.

در نمودارهای دایرهای، هر بخش از دایره نشان‌دهنده سهم یک بخش از اطلاعات، در مقایسه با کل آن اطلاعات است.

جواب فعالیت صفحه ۱۲۸ فصل ۷ ریاضی پنجم دبستان

سارا اطلاعات جدول مقابل را از پایگاه اینترنتی سازمان هواشناسی دریافت کرده است. این اعداد نشان‌دهنده بیشترین دمای ثبت‌شده در شهر کرمان در طول هفته گذشته هستند.

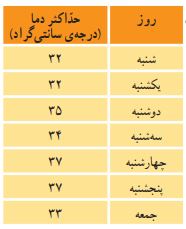
سارا قصد دارد نموداری خطی از این اطلاعات رسم کند.
الف) لطفاً محورهای افقی و عمودی نمودار را تکمیل کنید.
ب) طبق دستورالعمل‌های زیر، کار کشیدن نمودار را ادامه دهید:
– بخش‌هایی از نمودار که دما در حال افزایش است را با رنگ قرمز بکشید.
– بخش‌هایی که دما در حال کاهش است را با رنگ آبی نمایش دهید.
– قسمت‌هایی که دما ثابت مانده و تغییری نکرده است را با رنگ مشکی رسم کنید.

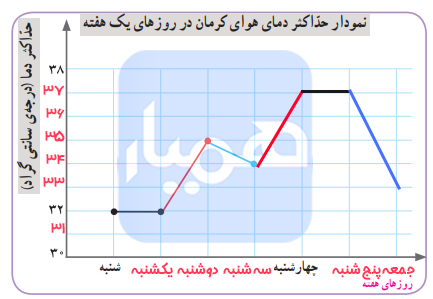
از شنبه تا یکشنبه، میزان ثابت ماند و تغییری نکرد.
از یکشنبه تا دوشنبه، افزایش داشت.
از دوشنبه تا سه‌شنبه، با کاهش روبرو شد.
از سه‌شنبه تا چهارشنبه، دوباره افزایش پیدا کرد.
از چهارشنبه تا پنج‌شنبه، بدون تغییر باقی ماند.
از پنج‌شنبه تا جمعه، کاهش یافت.

در آستانه عید نوروز، وقتی مادرش در حال سبز کردن سبزه عید بود، محیا هم یک دانه لوبیا داخل یک گلدان کوچک کاشت. او سپس رشد دانه را زیر نظر گرفت و تغییرات آن را در روزهای دوم، چهارم و بقیه روزها یادداشت کرد.

محیا هر دو روز یکبار، قد گیاهش را اندازه می‌گرفت و عدد آن را یادداشت می‌کرد. سپس این اعداد را در یک جدول مرتب کرد و با کمک آن‌ها، نمودار خطی که می‌بینید را کشید.

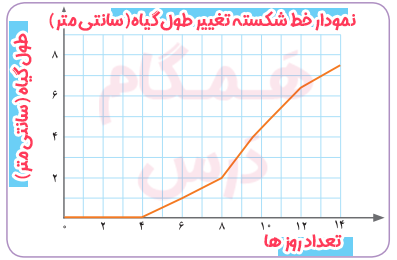
الف) عنوان‌های مناسب برای نمودار و محورهای آن انتخاب کنید.
ب) بین کدام دو روز، گیاه بیش‌ترین مقدار رشد را داشته است؟ این بخش از نمودار را مشخص کنید.
بین روزهای هشتم تا دهم.

جواب صفحه ۱۲۹ فصل هفتم ریاضی پنجم

برای جمع‌آوری اطلاعات، راه‌های گوناگونی وجود دارد؛ مانند نگاه کردن، پرسیدن، استفاده از برگه‌های پرسش، رجوع به کتاب‌ها یا پایگاه‌های اینترنتی و سنجش.
برای هر یک از موضوعات زیر، چه روشی برای جمع‌آوری اطلاعات مناسب است؟

الف) تعداد خواهر و برادرهای هر دانش‌آموز کلاس → برگه پرسش
ب) فاصله هر سیاره از خورشید در منظومه شمسی → رجوع به کتاب‌ها یا سایت‌ها
پ) تعداد دانش‌آموزانی که با کلاه به مدرسه می‌آیند → نگاه کردن
ت) مقدار بارندگی یک شهر در هر ماه از سال → سنجش
ث) فعالیت‌های خارج از مدرسه هر دانش‌آموز و زمان اختصاص‌یافته به هر فعالیت → پرسیدن
ج) سهم هر یک از گازهای موجود در هوا → رجوع به کتاب‌ها یا سایت‌ها

برای نمایش اطلاعات نیز می‌توان از جدول، نمودار ستونی، نمودار تصویری، نمودار خطی، نمودار دایره‌ای و موارد مشابه استفاده کرد.
به نظر شما برای نمایش اطلاعات هر موضوع بالا، کدام نوع نمودار مناسب است؟

– نمودار ستونی
– جدول یا نمودار تصویری
– نمودار ستونی
– نمودار خطی
– نمودار دایره‌ای
– نمودار دایره‌ای

اطلاعات مربوط به میزان برق مصرفی خانه‌ها در ایران طی ده سال، تقریباً در جدول زیر ارائه شده است. با انتخاب یک مقیاس مناسب و نقطه شروع درست، این اطلاعات را با استفاده از یک نمودار خطی نمایش دهید.

فاطمه در مورد این موضوع تحقیق کرد که دانش‌آموزان چه شماره‌تلفن‌های ضروری را به خاطر دارند. او از ۲۰ دانش‌آموز پرسش کرد و پاسخ‌های آن‌ها را در یک جدول ثبت کرد.

الف) یک نمودار میله‌ای بکشید که نشان دهد چند نفر از دانش‌آموزان هر شماره ضروری را بلد هستند.
(حتماً برای محور افقی و عمودی نمودار عنوان مناسب قرار دهید.)

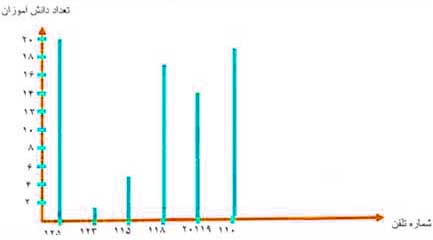
خیر، استفاده از نمودار خط شکسته برای این داده‌ها مناسب نیست. چون هدف از رسم این نمودار، نشان دادن تغییرات و روند یک چیز در طول زمان نیست. در واقع در اینجا، بررسی چگونگی تغییرات یک موضوع، مد نظر قرار ندارد.

جواب فعالیت صفحه ۱۳۰ و ۱۳۱ ریاضی پنجم دبستان

با استفاده از تعدادی حلقه، دو ستون در مقابل هم ساخته‌ایم. هدف این است که با همان حلقه‌ها، دو ستون بسازیم که ارتفاع یکسانی داشته باشند. در ادامه، راه حل دو دانش‌آموز ارائه شده است. یکی از این روش‌ها را انتخاب کنید و با کمک آن، جواب مسئله را پیدا کنید.

یکی از این روش‌ها را انتخاب کن تا به جواب برسی.

* در شکل سمت راست، ابتدا تمام حلقه‌ها را از ستون‌ها برمی‌داریم. سپس در هر مرحله، همزمان روی هر ستون یک حلقه قرار می‌دهیم. این کار را آنقدر تکرار می‌کنیم تا همه حلقه‌ها دوباره روی ستون‌ها چیده شوند.
* در شکل سمت چپ، از ستونی که حلقه‌های بیشتری دارد، به تدریج و یکی‌یکی حلقه برمی‌داریم و به ستون دیگر منتقل می‌کنیم. این کار را ادامه می‌دهیم تا زمانی که تعداد حلقه‌ها در هر دو ستون با هم برابر شود.

٢ــ در یک کارخانه که آبمیوه طبیعی تولید می‌کند، میزان آبی که از فشردن شش عدد سیب به‌دست می‌آید اندازه‌گیری شده و نتیجه در جدول زیر نوشته شده است.

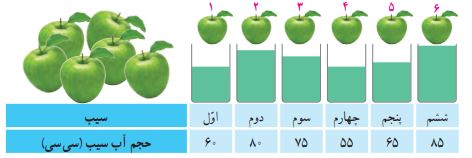
میانگین میزان آب موجود در شش عدد سیب را به این صورت محاسبه کرده‌اند. روش کار این است: ابتدا مقدار آب هر یک از سیب‌ها را با هم جمع می‌زنیم، سپس حاصل جمع به‌دست‌آمده را بر تعداد سیب‌ها (که شش عدد است) تقسیم می‌کنیم.

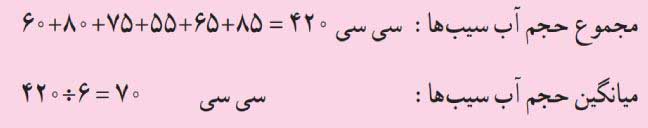
به شکل‌های زیر با دقت نگاه کنید. سپس توضیح دهید چطور می‌توانیم با استفاده از این شکل‌ها، میانگین حجم آب این شش سیب را محاسبه کنیم.

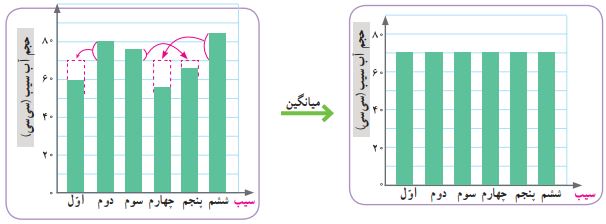
برای محاسبه میانگین داده‌ها از روی نمودار ستونی، باید ارتفاع همه ستون‌ها را با هم برابر کنیم. وقتی ارتفاع ستون‌ها یکسان شد، آن مقدار ثابت، نمایانگر میانگین داده‌ها خواهد بود. در نموداری که حجم آب سیب‌ها را نشان می‌دهد، پس از یکسان‌سازی ارتفاع ستون‌ها، مقدار ۷۰ سی‌سی به‌دست می‌آید. بنابراین میانگین حجم آب هر سیب، برابر با ۷۰ سی‌سی است.

پ) یک کارخانه آب‌میوه قصد دارد آب سیب را در بطری‌های ۷۰۰ سی‌سی بسته‌بندی کند. به نظر شما برای پر کردن هر بطری، تقریباً چند سیب لازم است؟ دلیل خود را بیان کنید.

با توجه به اینکه میانگین حجم آب هر سیب ۷۰ سی‌سی است، برای پر کردن یک بطری ۷۰۰ سی‌سی، حدود ۱۰ سیب مورد نیاز خواهد بود.

جواب کار در کلاس صفحه ۱۳۱ ریاضی پنجم دبستان

زهرا از پنج نفر از دوستانش پرسید که هر کدام چند کتاب داستان دارند و جواب‌ها را در یک جدول نوشت.

الف) میانگین تعداد کتاب‌ها چقدر است؟
برای محاسبه میانگین، تعداد کل کتاب‌ها را بر تعداد دوستان تقسیم می‌کنیم:
۳۰ = ۶ + ۹ + ۳ + ۷ + ۵
۶ = ۵ ÷ ۳۰
پس میانگین تعداد کتاب‌ها برابر با ۶ است.

ب) کدام دوستان کتاب‌های بیشتری از میانگین دارند؟
شادی، مهتاب و نیلوفر کتاب‌هایی بیشتر از میانگین دارند.

۲- سه مجموعه عدد مثال بزنید که میانگین آن‌ها ۱۰ شود. جواب خود را با بقیه مقایسه کنید.
مثال‌ها:
۱۰ ،۱۱ ،۹
۱۰ ،۱۵ ،۵
۱۰ ،۱۴ ،۶

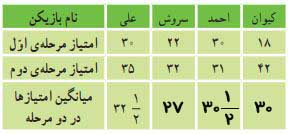
۳- گروهی از بچه‌ها در یک بازی دو مرحله‌ای شرکت کردند. امتیازهای آن‌ها در جدول زیر آمده است. مانند نمونه جدول را کامل کنید.
۵۴ = ۲۲ + ۳۲
۲۷ = ۲ ÷ ۵۴

جواب فعالیت صفحه ۱۳۲ فصل ۷ ریاضی پنجم دبستان

آقای حکیمی یک مزرعه پرورش مرغ دارد که در آن تعداد کمی مرغ نگهداری می‌کند. هر روز، او تخم‌مرغ‌های تازه را جمع‌آوری کرده و به بازار می‌برد تا بفروشد. همچنین هر روز، او وزن پنج عدد از تخم‌مرغ‌ها را اندازه‌گیری و ثبت می‌کند. تصویر مقابل، یکی از صفحات دفتر یادداشت آقای حکیمی را نشان می‌دهد.

الف) آقای حکیمی برای محاسبه میانگین وزن تخم‌مرغ‌های روز شنبه از یک روش ساده و جالب استفاده کرده است. مراحل روش او را در ادامه کامل کنید:

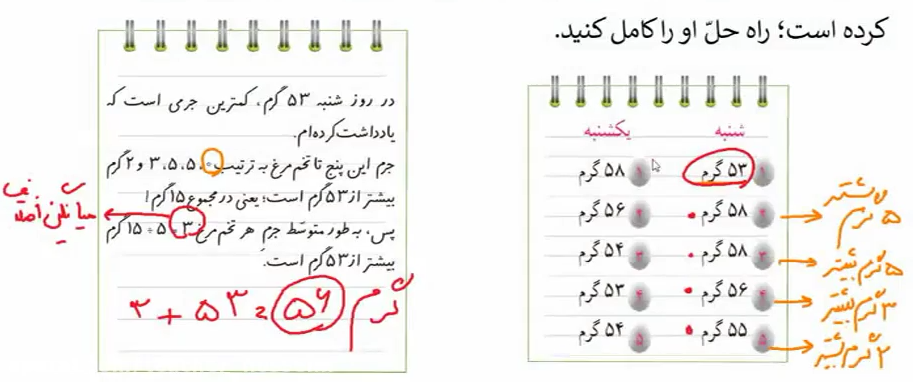
میانگین وزن تخم مرغ‌های روز شنبه را با روش قبلی محاسبه کنید. سپس نتیجه را با پاسخی که از روش جدید به دست می‌آید، مقایسه نمایید.
۳ = ۵ ÷ ۱۵ = ۰ + ۵ + ۵ + ۳ + ۲

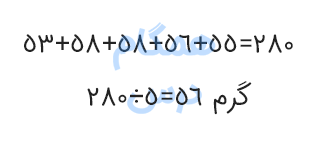
با استفاده از نمودار ستونی ارائه شده، می‌توانید صحت و کارآمدی روش جدید را ثابت کنید.

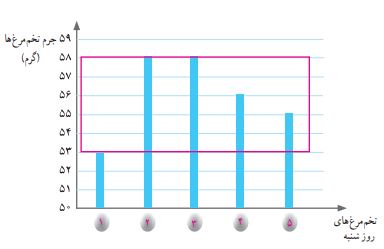
برای محاسبه میانگین داده‌ها از روی یک نمودار ستونی، کافی است ارتفاع تمام ستون‌ها را با هم برابر در نظر بگیریم.

ت) لطفاً میانگین وزن تخم‌مرغ‌های روز یکشنبه را به روشی که خودتان ترجیح می‌دهید محاسبه کنید. پاسخ این سؤال در تصویر بالا موجود است.

ابتدا تفاوت وزن هر تخم‌مرغ را از سبک‌ترین تخم‌مرغ که ۵۳ گرم است، محاسبه می‌کنیم. سپس این تفاوت‌ها را با هم جمع می‌زنیم و بر تعداد تخم‌مرغ‌ها که ۵ عدد است، تقسیم می‌کنیم.
میانگین تفاوت‌ها می‌شود:
(۱ + ۰ + ۱ + ۳ + ۵) ÷ ۵ = ۱۰ ÷ ۵ = ۲

در نهایت، میانگین وزن تخم‌مرغ‌ها در روز یکشنبه از جمع سبک‌ترین وزن (۵۳ گرم) و میانگین تفاوت‌ها (۲ گرم) به دست می‌آید:
۵۵ = ۲ + ۵۳

جواب تمرین صفحه ۱۳۳ فصل هفتم ریاضی پنجم دبستان

علی توانسته ۴۶۰ سانتیمتر مسیر را در ۱۰ قدم طی کند. میانگین طول هر قدم او چقدر است؟
۴۶ = ۱۰ ÷ ۴۶۰

دانشآموزان کلاس پنجم، کاغذهای باطله‌ای را که طی یک هفته در مدرسه دور ریخته شده بود، جمع‌آوری کردند. آنها می‌خواهند با کمک این اطلاعات نشان دهند که اگر کاغذهای دورریز در طول سال تحصیلی بازیافت شوند، از قطع شدن چه تعداد درخت جلوگیری می‌شود. داده‌های تقریبی این موضوع در نمودار زیر آورده شده است.

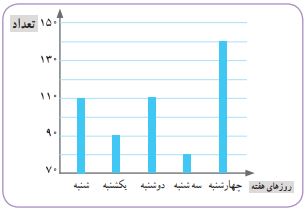
الف) بیشترین تعداد کاغذهای باطله در چه روزی بوده است؟
روز چهارشنبه.

ب) به طور تقریبی، چند تا کاغذ در آن روز دور ریخته شد؟
تقریباً ۱۴۰ برگه.

پ) میانگین تعداد کاغذهای باطله در هر روز این هفته چقدر است؟
جمع کل کاغذها: ۱۴۰ + ۸۰ + ۱۱۰ + ۹۰ + ۱۱۰ = ۵۳۰
میانگین: ۵۳۰ تقسیم بر ۵ روز برابر است با ۱۰۶

۳- محمد در یک بازی ۲۰ بار تاس ریخته و نتیجه هر بار را روی کاغذ نوشته است.

الف) کدام اعداد بیشتر از بقیه دیده شده‌اند؟ اعداد ۲ و ۵
ب) کدام عدد کمتر از همه تکرار شده؟ عدد ۳

۴- میانگین چهار عدد ۱۸، ۱۹، ۲۰ و ۲۷ را محاسبه کنید.
ابتدا این چهار عدد را با هم جمع می‌کنیم:
۸۴ = ۱۸ + ۱۹ + ۲۰ + ۲۷
سپس حاصل را بر تعداد آن‌ها تقسیم می‌کنیم:
۲۱ = ۴ ÷ ۸۴

۵- تیم فوتبال مدرسه در ۶ بازی گذشته به ترتیب ۲، ۴، ۳، ۰، ۵ و ۲ گل زده است. در بازی هفتم چند گل باید بزند تا میانگین گل‌هایش در این هفت بازی برابر با ۳ شود؟
می‌دانیم:
۳ = ۷ ÷ (؟ + ۲ + ۵ + ۰ + ۳ + ۴ + ۲)
پس:
۷ × ۳ = (؟ + ۲ + ۵ + ۰ + ۳ + ۴ + ۲)
۲۱ = (؟ + ۱۶)
بنابراین:
؟ = ۲۱ − ۱۶ = ۵

۶- میانگین چهار عدد متفاوت برابر ۱۰ است.
الف) مجموع این چهار عدد چقدر است؟
۴ × ۱۰ = ۴۰

ب) اگر بزرگترین عدد ۲۵ و کوچکترین آن ۲ باشد، دو عدد دیگر ممکن است چه اعدادی باشند؟
مثال‌هایی از جفت اعداد ممکن:
۱۰ و ۳، ۴ و ۹، ۵ و ۸، ۶ و ۷

 

جواب فعالیت صفحه ۱۳۴ ریاضی پنجم دبستان

وقتی می‌خواهیم در مورد اتفاقی که ممکن است رخ دهد صحبت کنیم، از کلماتی مانند «شاید»، «احتمال دارد» یا «ممکن است» استفاده می‌کنیم.
مثلاً:
– پریدن من به اندازه پنجاه متر، قطعاً امکان‌پذیر نیست.
– احتمال آمدن پدرم به مدرسه فردا صبح، کم است.
– شانس بردن یا باختن در مسابقه بعدی، مساوی است.
– چون خیلی تلاش کرده‌ام، به احتمال زیاد می‌توانم مسئله بعدی را حل کنم.
– یک مربع قطعاً چهار ضلع دارد.

حالا شما هم با این کلمات جمله‌هایی بسازید:
– احتمال دارد فردا باران ببارد.
– احتمال کمی دارد که ساعت ۱۰ صبح خواب باشم.
– قطعاً اتفاق نمی‌افتد که جمعه به مدرسه بروم.
– شاید با مادرم به بازار رفتم.
– اگر سکه بیندازم، به احتمال برابر «پشت» می‌آید.
– قطعاً امروز چهارشنبه است.
– ممکن است برای ناهار قرمه‌سبزی داشته باشیم.

یک پاکت بردارید و تعدادی دکمه همشکل و هم‌اندازه، با رنگ‌هایی که در تصویر می‌بینید، داخل آن بریزید. (اگر دکمه ندارید، می‌توانید دایره‌های هم‌اندازه از مقوا ببرید و رنگ کنید.)
قرار است بدون نگاه کردن داخل پاکت، یک دکمه از آن بیرون بکشید.
الف) برای هر اتفاق، احتمال رخ دادن آن را مانند نمونه روی نوار علامت بزنید.

هر بار، بدون اینکه داخل پاکت را ببینی، یک دکمه از آن بردار. رنگ دکمه‌ای را که بیرون آوردی، با کشیدن یک خط در جدول روبرو یادداشت کن. سپس، دکمه را دوباره داخل پاکت بگذار. این کار را بیست بار تکرار کن و در پایان، تعداد دفعاتی که هر رنگ را دیده‌ای در جدول بنویس.

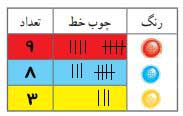
نتایجی که همه دانش‌آموزان کلاس به دست آورده‌اند را جمع‌آوری کنید و در جدول مقابل قرار دهید.
در کلاسی که ۳۰ دانش‌آموز دارد.

نتایج به دست آمده را با پاسخ‌های خود در بخش الف مقایسه کنید.
در هر دو حالت، شانس بیرون آمدن مهره‌ها یکسان است.

جواب کار در کلاس صفحه ۱۳۵ ریاضی پنجم دبستان

برای هر یک از گردونه‌های زیر، عقربه را می‌چرخانیم.
احتمال اینکه عقربه روی رنگ سبز توقف کند، با کدام عبارت نشان داده می‌شود؟ آن را مانند مثال مشخص کنید.

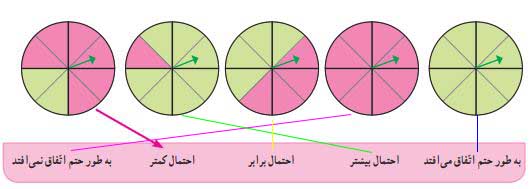
با استفاده از رایانه، یک چرخ‌وشانس مانند شکل زیر ساختیم و آن را ۱۰۰۰۰ بار چرخاندیم. نتایج این آزمایش در جدول زیر نشان داده شده است.

الف) اعداد تقریبی را در جدول وارد کنید و نمودار دایره‌ای مربوط به این داده‌ها را تکمیل نمایید.

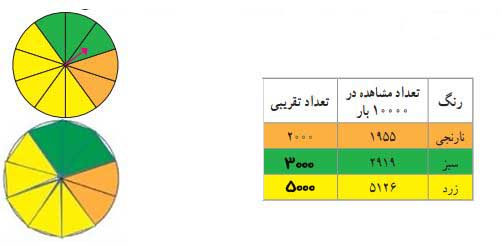
ب) نمودار دایره‌ای و چرخنده چه ویژگی مشترکی دارند؟
این دو کاملاً شبیه به هم هستند.

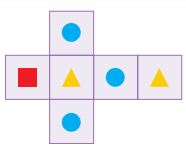
۳- با استفاده از الگوی داده‌شده، یک تاس مکعبی می‌سازیم. اگر تاس را پرتاب کنیم، کدام شکل احتمال بیشتری برای دیده شدن دارد؟
شکل دایره آبی، چون تعداد آن از بقیه بیشتر است.

جواب فعالیت صفحه ۱۳۶ ریاضی پنجم دبستان

یک تیم دو نفره بسازید. یک سکه و یک مهره بردارید و این بازی را شروع کنید.

کنار هم بنشینید و مشخص کنید که کدام یک از شما در سمت راست و کدام یک در سمت چپ قرار دارد. مهره را دقیقاً در خانه وسط بگذارید.
سکه را پرتاب کنید؛ اگر شیر آمد، مهره را یک خانه به سمت راست حرکت دهید و اگر خط آمد، مهره را یک خانه به سمت چپ ببرید.
برنده بازی کسی است که مهره زودتر به خانه او برسد.
پس از پایان، نتیجه بازی را در کلاس بیان کنید و آن را با نتایج گروه‌های دیگر مقایسه نمایید.
این بازی بر پایه شانس طراحی شده است. در یک بازی شانسی، اگر شانس برنده شدن همه بازیکنان برابر باشد، بازی عادلانه محسوب می‌شود.
به نظر شما این بازی عادلانه است؟
بله، چون احتمال برنده شدن هر دو بازیکن یکسان است.

جواب کار در کلاس صفحه ۱۳۶ ریاضی پنجم دبستان

بازی‌های زیر را بررسی کنید. اگر بازی عادلانه است، کنار آن علامت ✔️ بگذارید. اگر عادلانه نیست، بنویسید کدام بازیکن شانس بیشتری برای بردن دارد.

الف) یک سکه را پرتاب می‌کنیم. اگر شیر آمد، بازیکن اول برنده می‌شود و اگر خط آمد، بازیکن دوم.
این بازی ✔️ عادلانه است.

ب) یک تاس می‌اندازیم. اگر عدد ۱، ۲، ۳ یا ۴ بیاید، بازیکن اول برنده است و در غیر این صورت، بازیکن دوم.
این بازی عادلانه نیست و احتمال بردن بازیکن اول بیشتر است.

پ) عقربه چرخندهی مقابل را می‌چرخانیم. اگر عقربه روی رنگ سبز بایستد، بازیکن اول برنده است و اگر روی رنگ بنفش بایستد، بازیکن دوم.
این بازی ✔️ عادلانه است.

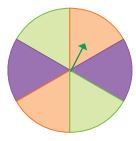
در بازی اول، عقربه‌ای داریم که می‌چرخد. اگر عقربه روی رنگ سبز بایستد، بازیکن اول برنده می‌شود و اگر روی رنگ دیگری بایستد، نفر دوم برنده خواهد شد. این بازی منصفانه نیست، چون شانس برنده شدن بازیکن دوم بیشتر است.

در بازی دوم، ما ۲۰ تیله داریم که می‌خواهیم داخل یک کیسه بگذاریم. سپس بدون نگاه کردن، یک تیله از داخل کیسه بیرون می‌آوریم. اگر تیله آبی بود، بازیکن اول برنده است و اگر سبز بود، بازیکن دوم. حالا باید ببینیم چند تیله آبی و چند تیله سبز در کیسه بگذاریم تا بازی عادلانه شود.
برای اینکه بازی عادلانه باشد، باید تعداد تیله‌های آبی و سبز دقیقاً برابر باشد. پس از هر رنگ ۱۰ تیله در کیسه قرار می‌دهیم.

جواب تمرین صفحه ۱۳۷ ریاضی پنجم دبستان

مسعود و چند تا از دوست‌اش داشتند بازی می‌کردند. در طول بازی، مسعود نتیجه‌ای که تاس‌ها نشان می‌دادند را روی کاغذ یادداشت می‌کرد. خلاصه‌ی چیزهایی که مسعود نوشته بود، در یک جدول آورده شده است.

الف) در این بازی، چند بار تاس انداخته‌اند؟
تعداد کل دفعات تاس‌اندازی ۳۰ بار بوده است. این عدد از جمع اعداد زیر به دست می‌آید:
۳۰ = ۷ + ۸ + ۴ + ۱ + ۷ + ۳

ب) کدام عدد بیشتر از بقیه ظاهر شده است؟
عدد ۵ بیشتر از سایر اعداد دیده شده است.

پ) کدام دو عدد به تعداد یکسان ظاهر شده‌اند؟
اعداد ۲ و ۶ به تعداد برابر دیده شده‌اند.

۲ــ اگر یک سکه را ۵ بار پرتاب کنیم، آیا ممکن است هر ۵ بار روی بیاید؟
بله، این امکان وجود دارد.

۳ــ می‌خواهیم عقربه چرخان زیر را بچرخانیم. کدام یک از این دو نفر درست می‌گوید؟ چرا؟

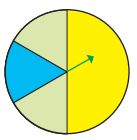
سینا: شانس توقف عقربه روی رنگ سبز از بقیه رنگ‌ها بیشتر است؛ چون دو بخش از چرخ، سبز است اما فقط یک قسمت زرد و یک قسمت آبی دارد. این حرف اشتباه است. ❌

مینا: احتمال اینکه عقربه روی رنگ زرد بایستد، از سایر رنگ‌ها بیشتر است؛ چون قسمت زردِ چرخ از بخش هر رنگ دیگری بزرگ‌تر است. این حرف درست است. ✅

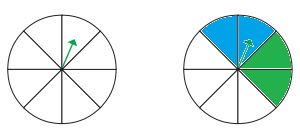
۴ــ چرخندهی زیر را طوری رنگ کنید که:
– احتمال توقف عقربه روی رنگ آبی و سبز یکسان باشد.
– احتمال توقف عقربه روی رنگ سفید از هر رنگ دیگری بیشتر باشد.

 

 

 

 جواب فرهنگ نوشتن صفحه ای  ۱۳۹ و ۱۳۸ ریاضی پنجم

۱ــ یک نمونه برای نمایش اطلاعات با نمودار خط شکسته، ثبت تغییرات دمای هوا در طول یک هفته است. میزان دمای محل زندگی خود را در یک هفته یادداشت کنید و آن را با نمودار خط شکسته نشان دهید.

۲ــ برای محاسبه میانگین چهار عدد، ابتدا آن‌ها را با هم جمع می‌کنیم و سپس حاصل را بر عدد ۴ تقسیم می‌کنیم. به عنوان مثال، برای اعداد ۲۱، ۲۷، ۱۳ و ۱۵:
[
21 + 27 + 13 + 15 = 76
]
[
76 div 4 = 19
]

۱- پنج عددی بنویسید که میانگین آن‌ها برابر با ۱۲ باشد. (سه پاسخ مختلف ارائه دهید.)
برای این کار، مجموع پنج عدد باید ۶۰ باشد، زیرا:
[
5 times 12 = 60
]
مثال‌ها:
(۲۰، ۱۲، ۴، ۹، ۱۵)، (۱۴، ۱۶، ۱۲، ۱۰، ۸)، (۱۲، ۱۲، ۱۲، ۱۲، ۱۲)

۲- سه عدد پشت سر هم (متوالی) بنویسید که میانگین آن‌ها ۱۵ باشد.
مثال‌ها:
(۱۵، ۱۵، ۱۵) و (۱۴، ۱۵، ۱۶)

۳- برای آسفالت کردن کوچه‌ای به عرض ۵ متر و طول ۱۰۰ متر، از ۵۰ تن آسفالت استفاده شده است. به طور متوسط، در هر متر مربع چند کیلوگرم آسفالت به کار رفته است؟
[
text{مساحت کوچه} = 5 times 100 = 500 text{متر مربع}
]
[
text{مقدار آسفالت بر حسب کیلوگرم} = 50 times 1000 = 50000 text{کیلوگرم}
]
[
text{مقدار آسفالت در هر متر مربع} = 50000 div 500 = 100 text{کیلوگرم}
]

۴- ثنا در سه مرحله از یک مسابقه به ترتیب ۱۸، ۱۵ و ۲۷ امتیاز کسب کرده است.
الف) میانگین امتیازهای او را حساب کنید.
[
18 + 15 + 27 = 60
]
[
60 div 3 = 20
]
ب) در مرحله چهارم، چه امتیازی کسب کند تا میانگین امتیازاتش تغییر نکند؟
[
4 times 20 = 80
]
[
80 – 60 = 20
]
پس باید در مرحله چهارم ۲۰ امتیاز کسب کند.

۵- مینا نماینده کلاس است. او تعداد غایب‌ها را در طول هفته گذشته یادداشت کرده است. میانگین تعداد غایب‌ها در هر روز را حساب کنید.

جمع تعداد دانش‌آموزانی که در روزهای مختلف غایب بودند به این صورت است: ۰ + ۱ + ۳ + ۰ + ۱ که می‌شود ۵ نفر.
میانگین غایب‌ها از تقسیم این مجموع بر تعداد روزها (۵ روز) به دست می‌آید:
۵ ÷ ۵ = ۱
یعنی به طور میانگین، هر روز یک نفر غایب بوده است.

حالا برای محاسبه‌ی میانگین اعداد ۰/۷، ۱/۱، ۲/۷ و ۳/۵، ابتدا آن‌ها را با هم جمع می‌کنیم:
۰/۷ + ۱/۱ + ۲/۷ + ۳/۵ = ۸
سپس مجموع را بر تعداد اعداد (۴ عدد) تقسیم می‌کنیم:
۴ ÷ ۸ = ۲
پس میانگین این اعداد برابر با ۲ است.

در یک مسابقه والیبال، دو تیم ۶ نفره از مدارس مختلف حضور دارند.
– کوتاه‌ترین بازیکن در تیم مدرسه فجر است با قد ۱۲۰ سانتی‌متر.
– بلندترین بازیکن در تیم مدرسه آزادی است با قد ۱۵۵ سانتی‌متر.
برای مقایسه، میانگین قد بازیکنان هر تیم محاسبه و با هم مقایسه می‌شود.

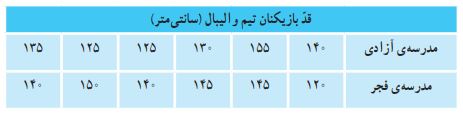
مدرسه آزادی:
جمع قد بازیکنان: ۱۳۵ + ۱۲۵ + ۱۳۵ + ۱۳۰ + ۱۵۵ + ۱۴۰ = ۸۱۰
میانگین قد: ۸۱۰ تقسیم بر ۶ نفر = ۱۳۵ سانتی‌متر

مدرسه فجر:
جمع قد بازیکنان: ۱۲۰ + ۱۴۵ + ۱۴۵ + ۱۴۰ + ۱۵۰ + ۱۴۰ = ۸۴۰
میانگین قد: ۸۴۰ تقسیم بر ۶ نفر = ۱۴۰ سانتی‌متر

همان‌طور که می‌بینید، میانگین قد بازیکنان تیم والیبال مدرسه فجر، ۵ سانتی‌متر از میانگین قد بازیکنان مدرسه آزادی بیشتر است. این یعنی به طور میانگین، هر بازیکن در تیم مدرسه فجر، ۵ سانتی‌متر از هر بازیکن در تیم مدرسه آزادی بلندتر است.

۸- پنج تیله سفید و پنج تیله نارنجی داریم. می‌خواهیم چهار تیله از آن‌ها را درون یک کیسه بریزیم و سپس بدون نگاه کردن، یک تیله از کیسه بیرون بیاوریم.
در هر حالت مشخص کنید چند تیله سفید و چند تیله نارنجی داخل کیسه بریزیم تا تیله‌ای که بیرون می‌آوریم:
الف) به احتمال زیاد سفید باشد. → ۴ تیله سفید و ۰ تیله نارنجی
ب) احتمال سفید بودنش کمتر از نارنجی بودنش باشد. → ۳ تیله نارنجی و ۱ تیله سفید
پ) احتمال سفید یا نارنجی بودنش برابر باشد. → ۲ تیله سفید و ۲ تیله نارنجی
ت) قطعاً سفید نباشد. → ۴ تیله نارنجی و ۰ تیله سفید

۹- می‌خواهیم با استفاده از الگوی داده‌شده یک تاس مکعبی بسازیم. روی هر وجه آن یکی از شکل‌های ☹️، 😐 یا 😊 را رسم می‌کنیم؛ به طوری که هنگام انداختن تاس، احتمال دیدن شکل 😊 از بقیه بیشتر و احتمال دیدن شکل ☹️ از بقیه کمتر باشد.
برای این کار می‌توان سه وجه را به شکل 😊، دو وجه را به شکل 😐 و یک وجه را به شکل ☹️ در نظر گرفت.