پاسخ تمرینهای فصل اول ریاضی پایهٔ هفتم
راهنمای گامبهگام فصل ۱ ریاضی هفتم

درس: راهبردهای حل مسئله | موضوع: آموزش گام به گام | پایه هفتم
در این بخش، پاسخ تمرینهای فصل اول ریاضی پایه هفتم را برای شما آماده کردهایم. موضوع این فصل، روشهای حل مسئله است. همچنین، راهنمای کامل این فصل به صورت فایل PDF نیز در دسترس شما قرار گرفته است.
برخی از بخشهای این فصل شامل موارد زیر است:
پاسخ تمرینها، فعالیتهای کلاسی و سوالات صفحات ۴ تا ۱۲ ریاضی هفتم از فصل اول.
جواب صفحه 2 درس اول ریاضی هفتم
انتخاب آسان صفحهها:
پاسخ صفحه ۲ درس اول ریاضی هفتم
پاسخ صفحه ۳ درس اول ریاضی هفتم
پاسخ صفحه ۴ درس اول ریاضی هفتم
پاسخ صفحه ۵ درس اول ریاضی هفتم
پاسخ صفحه ۶ درس اول ریاضی هفتم
پاسخ صفحه ۷ درس اول ریاضی هفتم
۱. یک باغچه به شکل مستطیل داریم که طول آن ۱۰ متر و عرض آن ۵ متر است. اگر بخواهیم از فاصله یک متری دور تا دور باغچه، نرده بکشیم، چه مقدار نرده نیاز داریم؟
راهنمایی:
– یک مستطیل رسم کنید.
– سپس در فاصله یک متری از هر ضلع، خطوطی موازی با اضلاع رسم کنید.
– با این کار یک مستطیل جدید و بزرگتر ایجاد میشود.
– طول و عرض این مستطیل جدید چقدر خواهد بود؟
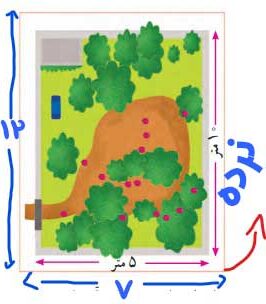
محیط مستطیل از جمع اندازه چهار ضلع آن به دست میآید.
در این حالت:
۱۲ متر + ۱۲ متر + ۷ متر + ۷ متر = ۳۸ متر
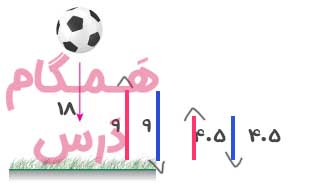
توپی از ارتفاع ۱۸ متری رها میشود. بعد از برخورد به زمین، تا نصف ارتفاع قبلی بالا میآید.
میخواهیم بدانیم از لحظهٔ شروع حرکت تا وقتی که برای سومین بار به زمین برخورد کند، چه مسافتی را طی کرده است.
– بار اول: از ارتفاع ۱۸ متر سقوط میکند (۱۸ متر).
بعد از زمینخوردن تا ارتفاع ۹ متر بالا میآید (۹ متر).
– بار دوم: از ۹ متر سقوط میکند (۹ متر).
بعد از زمینخوردن تا ارتفاع ۴/۵ متر بالا میآید (۴/۵ متر).
– بار سوم: از ۴/۵ متر سقوط میکند (۴/۵ متر) و به زمین میرسد.
حالا تمام مسیرهای رفت و برگشت را جمع میزنیم:
۱۸ (پایین) + ۹ (بالا) + ۹ (پایین) + ۴/۵ (بالا) + ۴/۵ (پایین) = ۴۵ متر
یک قورباغه میخواهد از یک دیوار صاف بالا برود. این دیوار ۹ متر ارتفاع دارد. قورباغه در هر بار پریدن ۳ متر به سمت بالا میجهد، اما بعد از هر پرش، ۲ متر به پایین لیز میخورد.
سؤال این است که این قورباغه پس از چند پرش به بالای دیوار میرسد؟
پاسخ: ۷ پرش.
جواب صفحه 3 درس اول ریاضی هفتم
دو عدد طبیعی پیدا کنید که وقتی در هم ضرب میشوند، حاصل ۲۴ شود و وقتی با هم جمع میشوند، کمترین مقدار ممکن را داشته باشند. برای این کار، جدول را به صورت منظم و مرحلهای کامل کنید.
کوچکترین عدد طبیعی کدام است؟ ۱
اگر ۱ را در چه عددی ضرب کنیم تا حاصل ۲۴ شود؟ ۲۴
حالا عدد طبیعی بعدی را در نظر بگیرید و به همین روش ادامه دهید تا تمام حالتهای ممکن را پیدا کنید.
| حاصل جمع | دومین عدد | اولین عدد |
| 1+24=25 | 24 | 1 |
| 2+12=14 | 12 | 2 |
| 3+8=11 | 8 | 3 |
| 4+6=10 کم ترین مقدار | 6 | 4 |
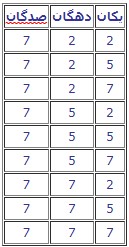
با انگشتان یک دست میتوان عدد ۱ را به پنج شکل مختلف نشان داد. حالا سوال این است که عدد ۲ را به چند روش میتوان با انگشتان یک دست نشان داد؟
| تعداد حالات | انگشت های جفت شده | انگشت ها |
| 4 حالت | (5، 1) (4، 1) (3، 1) (2، 1) | انگشت 1 |
| 3 حالت | (5، 2) (4، 2) (3، 2) | انگشت 2 |
| 2 حالت | (5، 3) (4، 3) | انگشت 3 |
| 1 حالت | (5، 4) | انگشت 4 |
| قبلا با همه جفت شده | انگشت 5 |
با انگشتان یک دست، میتوان عدد ۲ را به ده روش مختلف نشان داد.
همچنین، با استفاده از ارقام ۷، ۲ و ۵، تمام اعداد سهرقمی ممکن را بنویسید. توجه داشته باشید که در این اعداد، استفاده مجدد از یک رقم مجاز است.
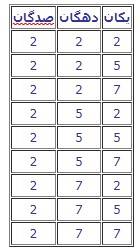
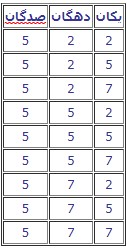
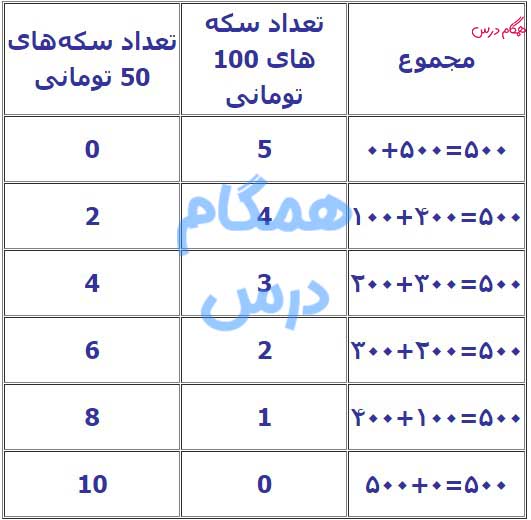
ما کلی سکه ۵۰ تومانی و ۱۰۰ تومانی داریم. میخواهیم بدانیم با چند روش مختلف میتوانیم کرایه تاکسی را که ۵۰۰ تومان است، پرداخت کنیم.
برای این کار باید ببینیم چند جور میتوانیم ترکیبی از سکههای ۵۰ تومانی و ۱۰۰ تومانی را طوری انتخاب کنیم که مجموع آنها دقیقاً ۵۰۰ تومان شود.
حالتهای ممکن عبارتند از:
– میتوانیم از ۱۰ سکه ۵۰ تومانی استفاده کنیم.
– میتوانیم از ۸ سکه ۵۰ تومانی و ۱ سکه ۱۰۰ تومانی استفاده کنیم.
– میتوانیم از ۶ سکه ۵۰ تومانی و ۲ سکه ۱۰۰ تومانی استفاده کنیم.
– میتوانیم از ۴ سکه ۵۰ تومانی و ۳ سکه ۱۰۰ تومانی استفاده کنیم.
– میتوانیم از ۲ سکه ۵۰ تومانی و ۴ سکه ۱۰۰ تومانی استفاده کنیم.
– میتوانیم از ۵ سکه ۱۰۰ تومانی استفاده کنیم.
پس در مجموع ۶ روش مختلف برای پرداخت کرایه ۵۰۰ تومانی وجود دارد.
جواب صفحه 4 درس اول ریاضی هفتم
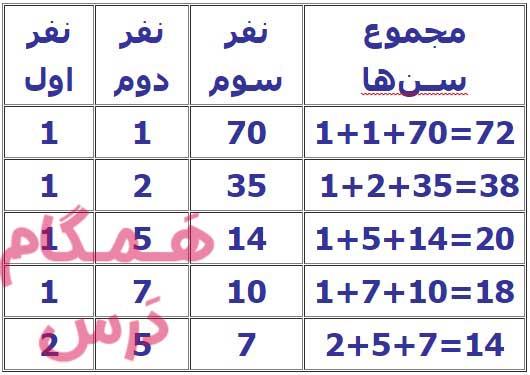
سن سه نفر با هم ۱۴ سال است و اگر سن آنها را در هم ضرب کنیم، حاصل ۷۰ میشود. میخواهیم بدانیم سن بزرگترین فرد چند سال است.
برای حل این مسئله، ابتدا باید تمام حالتهایی را پیدا کنیم که سه عدد طبیعی در هم ضرب شوند و حاصل ۷۰ شود. این حالتها را میتوان به صورت زیر نوشت:
– ۱، ۱، ۷۰
– ۱، ۲، ۳۵
– ۱، ۵، ۱۴
– ۱، ۷، ۱۰
– ۲، ۵، ۷
حالا باید ستونی به این جدول اضافه کنیم که مجموع سن هر سه نفر را نشان دهد. با این کار، فقط حالتی باقی میماند که مجموع سنها برابر ۱۴ باشد.
فرض کنید دوست شما یک عدد از ۰ تا ۹۹ انتخاب کرده است. شما باید با پرسیدن سوالهایی که فقط با «بله» یا «خیر» پاسخ داده میشوند، آن عدد را پیدا کنید.
در این حالت فقط یک عدد درست است و بقیه نادرست.
حالا میخواهیم بدانیم کدام سوال برای پیدا کردن عدد مناسبتر است.
– اگر بپرسید: «آیا عدد مورد نظر شما ۲۷ است؟»
اگر جواب «خیر» باشد، فقط عدد ۲۷ حذف میشود (یعنی فقط ۱ حالت نادرست حذف شده).
– اگر بپرسید: «آیا عدد مورد نظر شما زوج است؟»
اگر جواب «خیر» باشد، تمام اعداد زوج (۵۰ عدد) حذف میشوند (۵۰ حالت نادرست حذف شده).
– اگر بپرسید: «آیا عدد مورد نظر شما یکرقمی است؟»
اگر جواب «خیر» باشد، اعداد ۰ تا ۹ (۱۰ عدد) حذف میشوند (۱۰ حالت نادرست حذف شده).
– اگر بپرسید: «آیا عدد مورد نظر شما از ۵۰ بزرگتر است؟»
اگر جواب «خیر» باشد، اعداد ۵۱ تا ۹۹ (۴۹ عدد) حذف میشوند (۴۹ حالت نادرست حذف شده).
سوالی مناسبتر است که در صورت پاسخ «خیر»، تعداد بیشتری از حالتهای نادرست را حذف کند.
در اینجا سوال مربوط به زوج یا فرد بودن عدد بهتر است، چون نصف اعداد (۵۰ عدد) را حذف میکند.
جواب صفحه 5 درس اول ریاضی هفتم
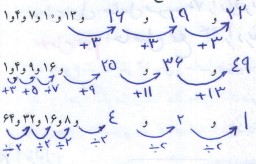
الگوی اول: ۲، ۴، ۶، ۸، ۱۰، …
اعداد بعدی: ۱۲، ۱۴، ۱۶
رابطه: هر عدد دو واحد از عدد قبلی بیشتر است.
الگوی دوم: ۱، ۴، ۹، ۱۶، ۲۵، …
اعداد بعدی: ۳۶، ۴۹، ۶۴
رابطه: هر عدد برابر است با مربع شمارهی خودش. مثلاً عدد سوم (۹) برابر است با ۳ ضربدر ۳.
الگوی سوم: ۱، ۳، ۶، ۱۰، ۱۵، …
اعداد بعدی: ۲۱، ۲۸، ۳۶
رابطه: هر عدد از جمع عدد قبلی با شمارهی خودش به دست میآید. مثلاً عدد چهارم (۱۰) برابر است با ۶ (عدد قبلی) به اضافهی ۴ (شمارهی آن).
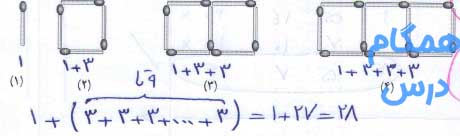
برای پیدا کردن تعداد چوب کبریتهای شکل دهم، به الگوی ساخت آن نگاه میکنیم.
اعداد به صورت سهتایی اضافه میشوند.
هر عدد طبیعی در خودش ضرب میشود.
سپس حاصل بر دو تقسیم میگردد.
شکل دهم با چند چوب کبریت درست میشود؟ چرا؟
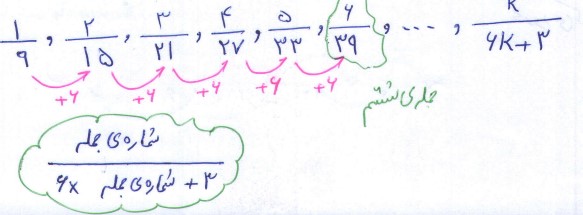
در شکل شماره ۱، یک قسمت از سه قسمت رنگی است. اگر این الگو ادامه پیدا کند، در شکل شماره ۶، چه بخشی از آن رنگی خواهد بود؟
جواب صفحه 6 درس اول ریاضی هفتم
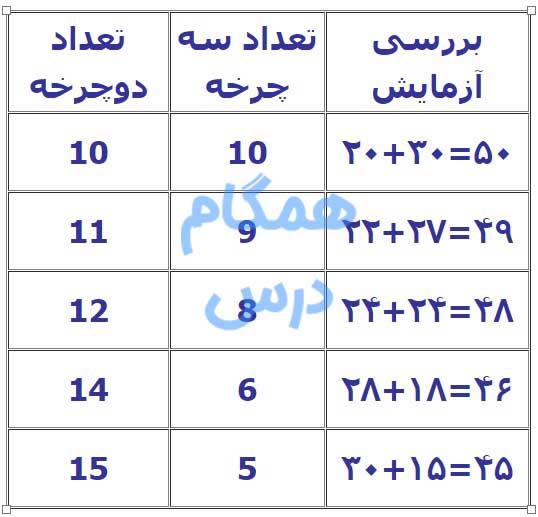
در یک پارکینگ، ۲۰ دستگاه دوچرخه و سهچرخه قرار دارد. اگر مجموع چرخهای آنها ۴۵ عدد باشد، چند دوچرخه و چند سهچرخه داریم؟
برای شروع، فرض کنید تعداد دوچرخهها ۱۰ و سهچرخهها هم ۱۰ دستگاه باشد.
حالا با کمک جدول، این فرض را آزمایش کنید.
با توجه به نتیجه آزمایش، باید تعداد سهچرخهها را بیشتر کنیم یا دوچرخهها؟ چرا؟
دو زاویه مکمل هستند. اگر یکی از آنها سه برابر دیگری باشد، اندازه هر زاویه چقدر است؟
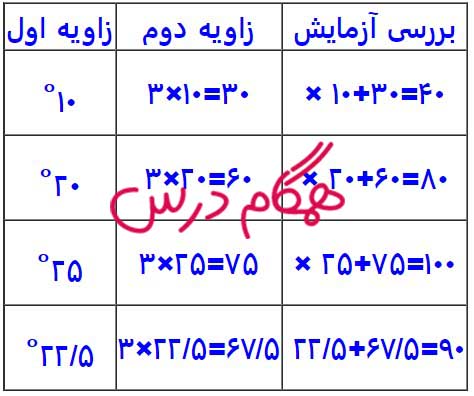
برای پیدا کردن عددی که باید به جای مربع آبی قرار دهیم، معادله را حل میکنیم.
میدانیم:
سه تا از آن عدد به اضافهی ده میشود سیویک.
پس اول عدد ده را از سیویک کم میکنیم:
31 – 10 = 21
حالا عدد ۲۱ را به سه قسمت مساوی تقسیم میکنیم (چون سه تا از آن عدد داریم):
21 ÷ 3 = 7
پس جواب عدد ۷ است.
| برسی🟦 | 3*🟦+10 | 🟦 |
| 🟦 را کاهش میدهیم | 3*10+10=40 | 10 |
| 🟦 را کاهش میدهیم | 3*9+10=37 | 9 |
| 🟦 را کاهش میدهیم | 3*8+10=34 | 8 |
| حدس درست است | 3*7+10=31 | 7 |
جواب صفحه 7 درس اول ریاضی هفتم
محمد هر هفته ۳۰۰۰ تومان پسانداز میکند. او حساب کرده که پول پنج هفته پساندازش، برابر با نصف قیمت کیف مورد علاقهاش است. قیمت کیف چقدر است؟
الف) پول پسانداز پنج هفته:
۱۵۰۰۰ = ۵ × ۳۰۰۰
تومان
ب) اگر این مبلغ نصف قیمت کیف باشد، قیمت کامل کیف میشود:
۳۰۰۰۰ = ۲ × ۱۵۰۰۰
تومان
طول یک استخر ۱۲ متر، عرض آن ۶ متر و عمق آن ۳ متر است. قرار است کف و تمام دیوارهای داخلی این استخر رنگ آمیزی شود. برای رنگ کردن هر متر مربع، ۰.۳ کیلوگرم رنگ لازم است. در کل چه مقدار رنگ برای این کار نیاز است؟
۱- محاسبه مساحت کف استخر:
۷۲ = ۶ × ۱۲
متر مربع
۲- محاسبه مساحت دیوارهای استخر:
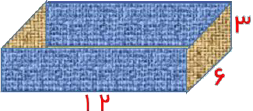
ابتدا محاسبات مربوط به استخر را انجام میدهیم:
۶ ضربدر ۳ میشود ۱۸ → سپس ۱۸ ضربدر ۲ میشود ۳۶
۱۲ ضربدر ۳ میشود ۳۶ → سپس ۳۶ ضربدر ۲ میشود ۷۲
مساحت کل استخر:
۷۲ + ۷۲ + ۳۶ = ۱۸۰
مقدار رنگ مورد نیاز:
۱۸۰ × ۰/۳ = ۵۴
—
حالا مسئله میوهفروشی را بررسی میکنیم:
میوهفروش امروز ۴۰ کیلوگرم سیب خرید. قیمت هر کیلوگرم سیب ۲۵۰۰ تومان بود.
همچنین ۸۰ کیلوگرم پرتقال خرید که قیمت هر کیلوگرم آن ۱۵۰۰ تومان بود.
او هر کیلوگرم سیب را ۳۰۰۰ تومان و هر کیلوگرم پرتقال را ۲۰۰۰ تومان فروخت.
میخواهیم بدانیم چقدر سود کرده است.
۱- سود از فروش هر کیلو سیب:
۳۰۰۰ − ۲۵۰۰ = ۵۰۰ تومان
۲- سود کل از فروش سیبها:
۴۰ × ۵۰۰ = ۲۰۰۰۰ تومان
۳- سود از فروش هر کیلو پرتقال:
۲۰۰۰ − ۱۵۰۰ = ۵۰۰ تومان
۴- سود کل از فروش پرتقالها:
۸۰ × ۵۰۰ = ۴۰۰۰۰ تومان
۵- سود کلی:
۲۰۰۰۰ + ۴۰۰۰۰ = ۶۰۰۰۰ تومان